Заключени кандидати тип 1 (Посочване)
Ако в една кутия всички кандидати за конкретно число са ограничени до един ред или колона, това число не може да присъства извън тази кутия в същия ред или колона.
Нека да погледнем примера, за да разберем Заключените Кандидати малко по-добре.
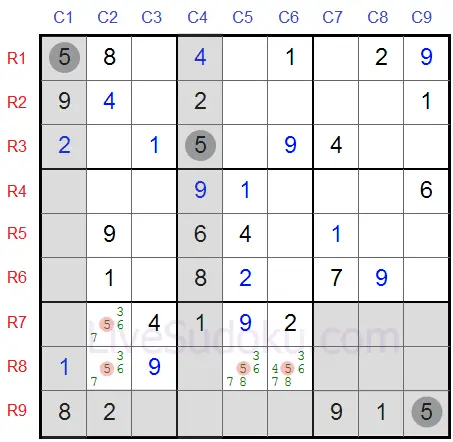
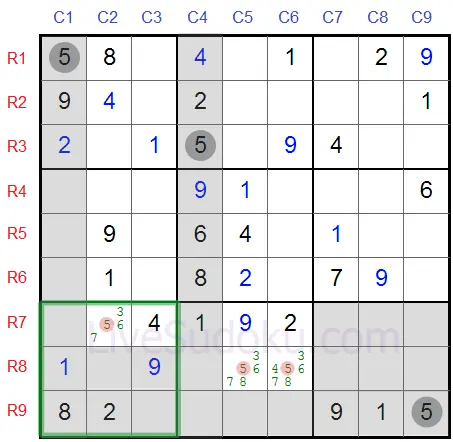
Вижте това Судоку.
Търсим възможните клетки за '5' в долните кутии, маркирани са в червено.
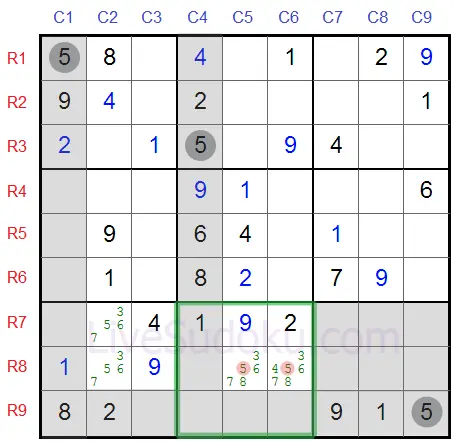
Сега погледнете в средно-долната кутия в частност - тази кутия трябва да съдържа '5'
Трябва да бъде или на R8C5 или на R8C6 и тези клетки са на един и същи ред - ред #8.
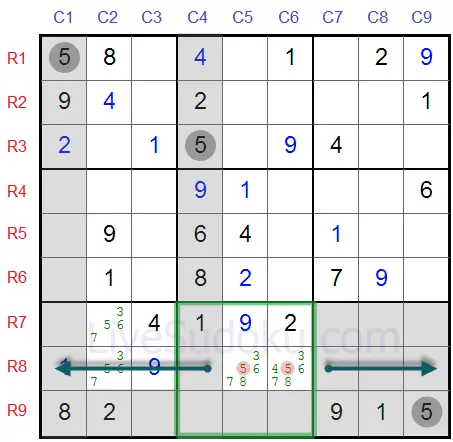
Това значи, че на ред #8 освен тези две клетки, никои други не могат да съдържат числото 5.
Едно число може да присъства само веднъж на всеки ред - а ние вече сме установили, че или R8C5 или R8C6 трябва да съдържат '5'.
Така можем да елиминираме 5 от всички други клетки в този ред, в частност R8C2.
Сега поглеждаме към кутия #7 (маркирана в полето).
Останал е само един кандидат за '5' - R7C2 - това е Скрита Единица и трябва да съдържа '5'.
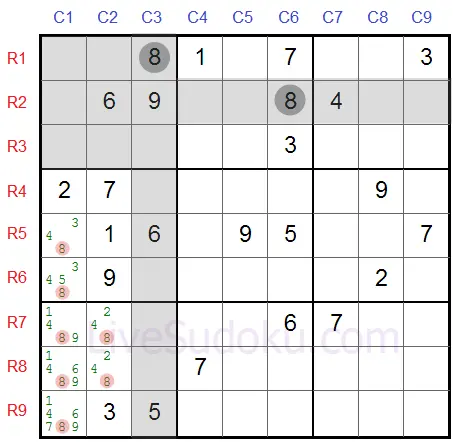
Нека да разгледаме друг пример, можете ли да видите заключения кандидат в този пример?
Съвет: този път е в колона.
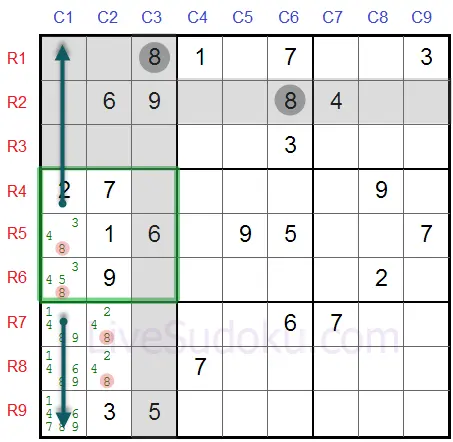
В средната-лява кутия, '8' трябва да бъде в R5C1 или в R6C1 - като и двете са в същата колона #1.
Това значи, че в колона #1 - никои други клетки, освен тези две могат да съдържат числото '8' - числото може да присъства само веднъж във всяка колона, а ние установихме, че R5C1 или R6C1 трябва да съдържат '8'.
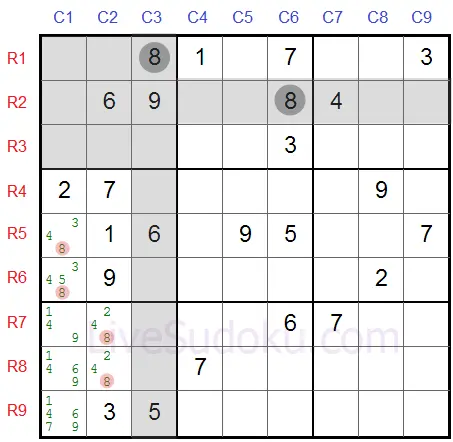
Значи можем да елиминираме '8' от всички други клетки в този ред - R7C1, R8C1 и R9C1.
Някои ходове като този помагат да елиминираме кандидати от клетки - вместо да решаваме клетките - което ще бъде постигнато чрез допълнителни ходове и методи.